秋らしくなってきました。山口は急に寒くなったためか、街路樹の葉が紅葉せずに落ちているところもあります。

　以前の記事で私は休日に軽いジョギングをしていることは何度もご紹介しました。いつも同じルートを走ると季節の移り変わりを感じることはできますが、やはり飽きます。そこで、たまに新鮮さを求めて新しいルートに変えてみると、自宅付近にもかかわらずとても景色が新鮮に感じられ、また新たな発見があります。しばらくそのルートを走るとまた飽きるので、次は逆向きに回ります。
　あるルートを逆向きに回ると、まったく違った景色が見え、別の発見があってもう一度楽しむことができます。（残念ながら「自宅」は私自身が湧き出し、吸い込まれる「特異点」であり、いつもあらゆる角度から眺めているのでなかなか新しい発見はありません。）
　私たち教員はしばしば学生に「物事はさまざまな角度から眺めることが大切です。自身の実験結果も別の視点で見れば、新しいことに気が付くこともあります。」とよく指導します。この言葉を理解してもらうには、実際に経験してもらうのが早いのですが、なかなか実験結果でよい例に恵まれません。ジョギングルートを逆向きに回ることも一つの例ですが、この例は少しお粗末ですね。

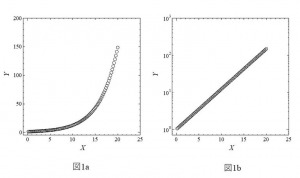図1aのグラフはxという量とyという量の関係を表しているとします。ｘが増加するとyも増加し、xの増加ともにyの増加の仕方がだんだんと急になっていることがわかります。大学1年生に実験で得たこのような関係を言葉で説明してもらうと、よくある回答が「放物線の関係」。それを起点に「放物線とはどのような曲線か？」などの問答が始まります。「ではこれが放物線であることの証拠を示してみてください。」と言うと、そこで気づく学生があり、そうでない学生もあり。図1bのグラフは図1bのグラフの縦軸(y)を対数目盛で表しています。直線になっています。yがxの指数関数であることがわかります。「放物線（yがxの2次関数）」ではありませんでした。

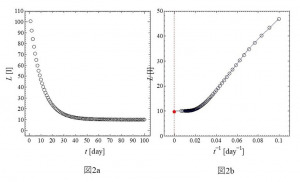　図2aは私が家に備蓄しているお酒の量が日ごとに減っていく様子を示しています。（もちろんフィクションです。）自制がかかり、空っぽになるのではなく、ある程度の量を残しておこうとしている魂胆がなんとなくわかります。いったいどの程度残しておこうとしているのでしょうか。横軸を時間の逆数に取り直すと図2bのようにt → ∞での残量がt^-1 = 0の時の量で推測されます。未来予測です。
　角度をかえて物事を見る、大事なことですね。

私の休日のジョギング、健康と気分転換が目的ですので、たまには趣向を変え、自転車で少し遠くまで。山口市の中心市街地にはこのような雰囲気のよい場所が多くあります。