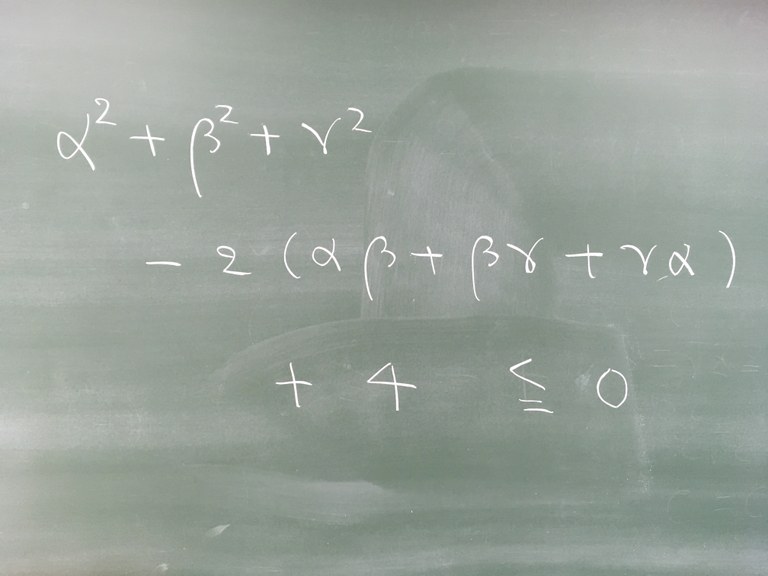
研究テーマ

リーマン面の正則写像

研究内容

リーマン面の正則写像の存在問題に取り組んでいます。リーマン面は，正則関数すなわち複素微分可能な関数をもっとも自然に考察することの出来る場として19世紀に天才数学者リーマンが考案した数学的対象で，現代数学の言葉を用いれば，連結な１次元複素多様体です。表裏の区別があり，各点で角度を測ることの出来る曲面と思ってください。すると，ひとつのリーマン面から他のリーマン面への非定値正則写像は，ほとんどの点で角度を保つ写像であると捉えることが出来ます。さて，実微分可能な場合と異なり，わずかな条件が強い制約をもたらしてしまうという現象がしばしば観察されます。例えば，半径１と半径３の同心円で囲まれた領域から半径４と半径８の同心円で囲まれた領域の中への正則写像で，前者の領域内の半径２の同心円の像が半径４の円を取り囲むように写すものは存在しません。このような現象を組織的に研究しています。

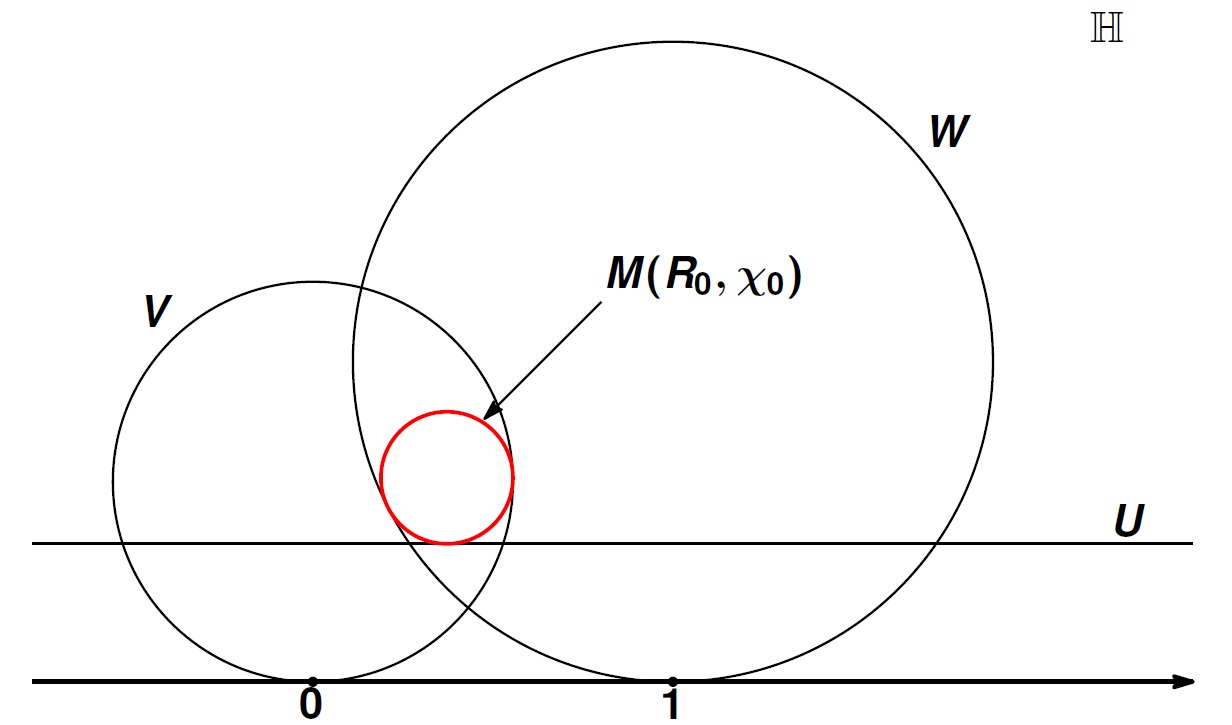
３つのホモロジー類の極値的長さがモディライ円板を決める

指導学生の修士論文・卒業論文題目

• Picardの定理について（2020年度・修士論文）
• 整関数の位数と零点の収束指数（2020年度・修士論文）
• 正則関数の自然境界について（2020年度・修士論文）
• Hardy空間について（2019年度・修士論文）
• 単位円板から単位円板の中への正則関数（2019年度・修士論文）
• 巡回符号について（2019年度・卒業論文）
• BHC符号（20219年度・卒業論文）

教員情報