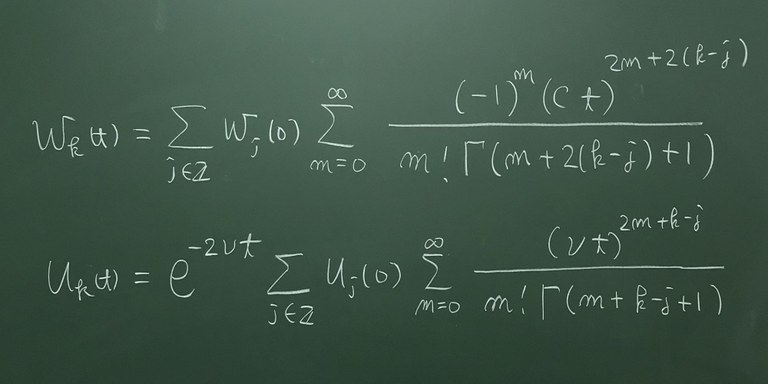
研究テーマ

数理物理に現れる線形および非線形偏微分方程式の研究

研究内容

わたしたちの身の回りにある様々な現象、たとえば天体の運動、大気の変動、地震の揺れの伝わり方、株価の変動、水面に観測される波、電子機器の中を流れる電流、素粒子の状態など、これらはすべて微分方程式を用いた数式によって記述されると考えられています。したがって、物理学や工学・経済学などの応用面から微分方程式は非常に重要な研究対象です。一方、解析学や代数学などの純粋数学の応用という面でも、微分方程式は世界中の多くの数学者が取り組んでいる極めて重要な研究対象です。このような微分方程式には、目的とする対象によって数多くの種類と研究の手法がありますが、私の研究対象は、主に「波動方程式」とよばれる、水面の起伏の変化や空気中を伝わる音、地震波や電磁波などを記述する偏微分方程式で、これらの方程式の解の性質を、微分積分学を基礎とする解析学的手法を用いて研究しています。

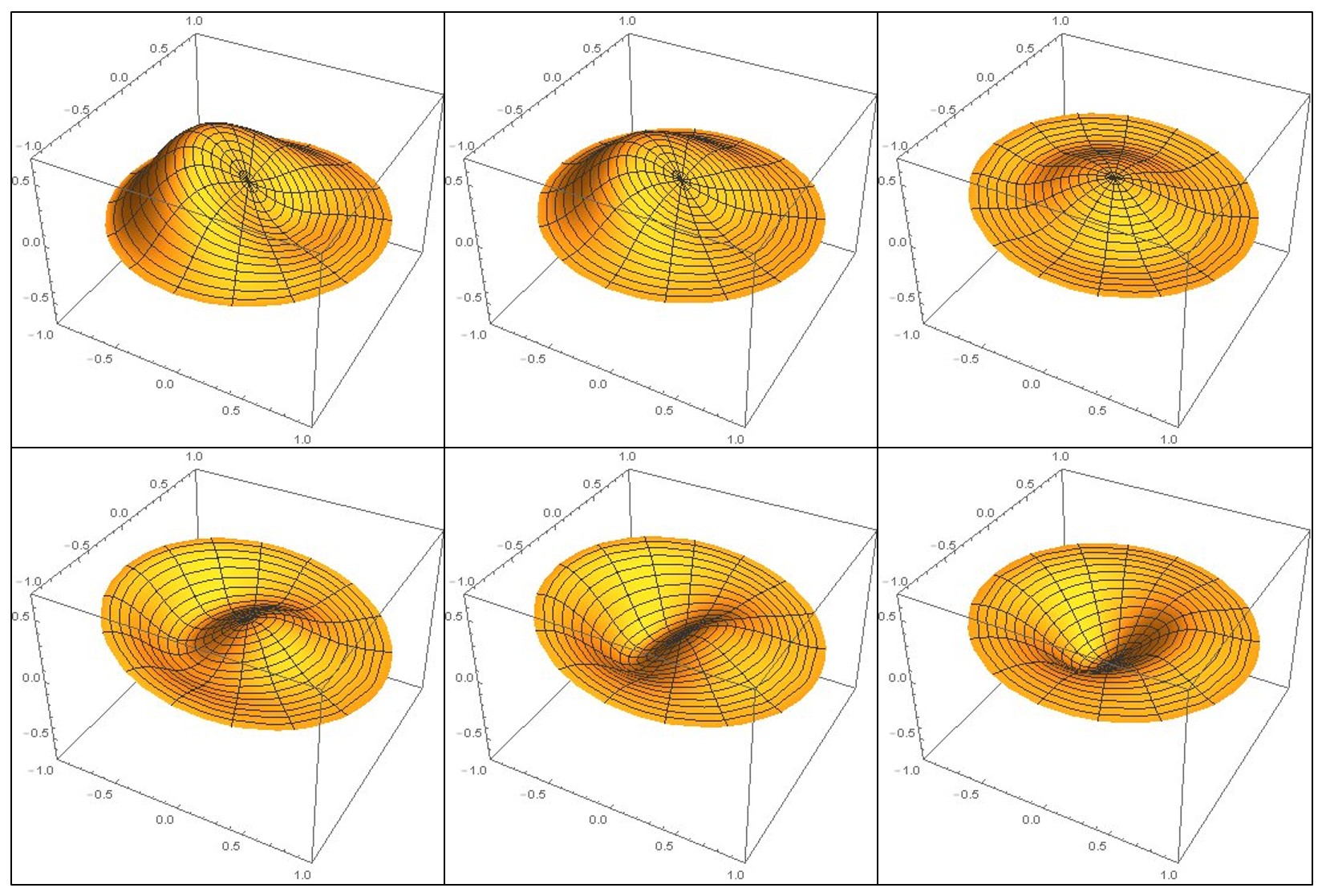
円領域での２次元波動方程式の解の時間変化（コップの中の水面の動きを表しています）

指導学生の修士論文・卒業論文題目

• 高次元波動方程式の初期値問題（2024年度・卒業論文）
• 直交関数展開とその応用（2024年度・卒業論文）
• 梁の自由振動における初期値境界値問題（2024年度・卒業論文）
• 弱消散型波動方程式の初期値問題のエネルギー評価（2024年度・修士論文）
• 1 次元半離散消散型波動方程式の初期値問題について（2024年度・修士論文）
• 星型グラフ上の Sturm-Liouville 問題（2024年度・修士論文）
• 数理物理の偏微分方程式（2024年度・修士論文）

教員情報

• E-mail：hirosawa@ (@以下はyamaguchi-u.ac.jp )
• Web Sites：http://ds0n.cc.yamaguchi-u.ac.jp/~hirosawa/indexj.htm
• Research Map：https://researchmap.jp/read0163109