研究テーマ

結び目の位相不変量の研究

研究内容

私の研究分野は位相幾何学に属する結び目理論であり，主な研究内容は不変量を開発したり，不変量を用いて結び目を分類したりすることです。結び目とは，3次元球面内の自己交差の無いねじれた輪のことを言います。2つの結び目に対して，3次元球面の向きを保存する自己同相写像が存在し，その写像により一方の結び目がもう一方の結び目に移されるとき，その2つの結び目は同型，すなわち，同じ結び目であると言います。大雑把に述べると，結び目理論の主要な研究目的はどの結び目とどの結び目が同じであるかを定めること，即ち，結び目を分類することです。結び目を分類するためには，通常，不変量と呼ばれる道具が用いられます。直下に2つの結び目の図があります。一方が自明な結び目と呼ばれる解けている結び目，もう一方が解けていない結び目です。これらは，不変量，例えば，結び目の種数，符号数，アレキサンダー多項式，ジョーンズ多項式などで区別されます。

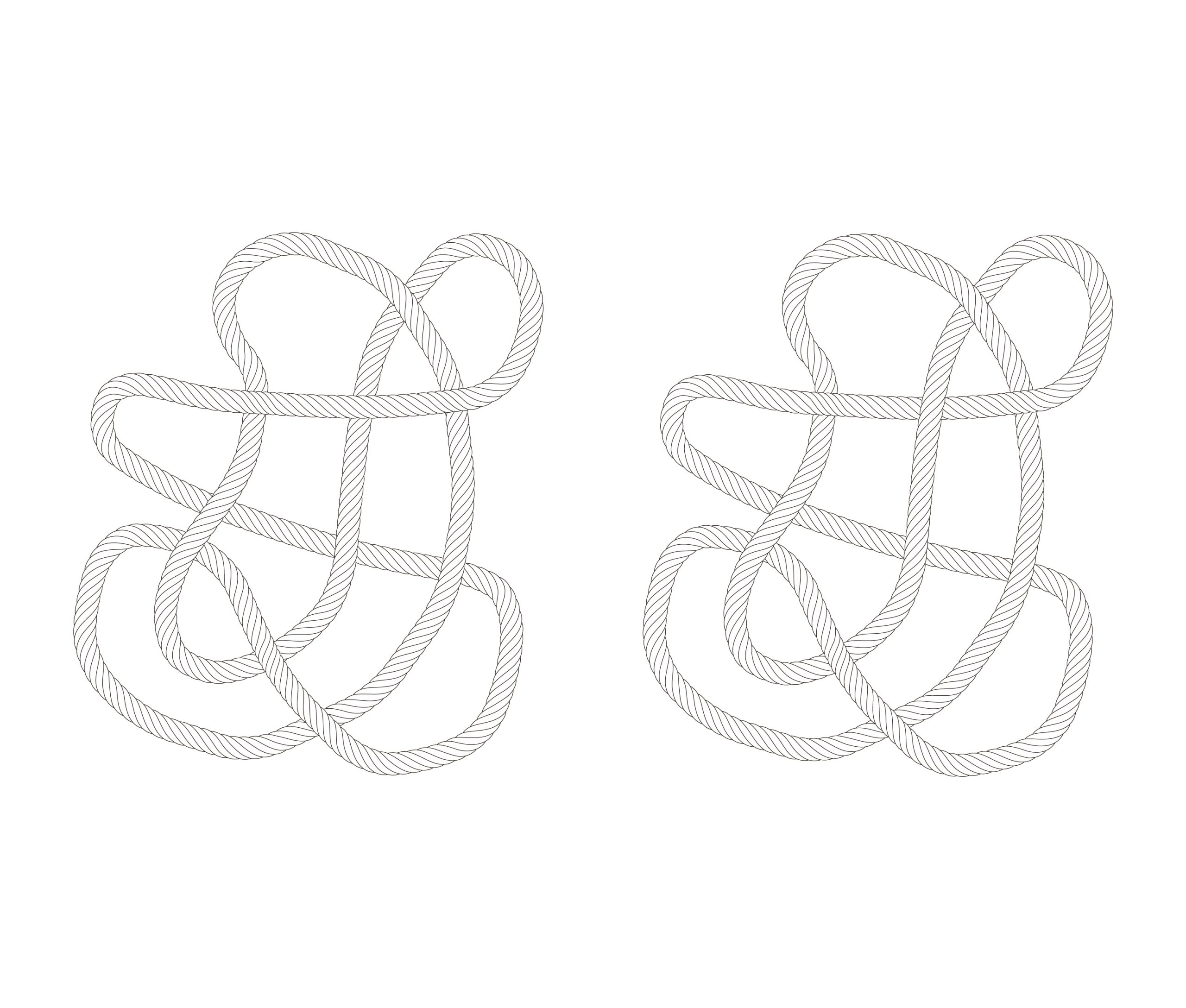
結び目の例： どちらが自明な結び目だろうか？

指導学生の修士論文・卒業論文題目

• アレキサンダー多項式が消えるタングルについて（2024年度・修士論文）
• プレッツェル絡み目のジョーンズ多項式について（2024年度・修士論文）
• 結び目の局所変形とジョーンズ多項式（2024年度・修士論文）
• プレッツェル結び目のアレキサンダー多項式について（2023年度・修士論文）
• 自明なアレキサンダー多項式と対称性を持つ絡み目について （2023年度・修士論文）
• グラフが内蔵する絡み目について（2022年度・修士論文）
• 結び目の対称和と鏡像積の多項式不変量について（2021年度・修士論文）
• 折り紙を用いた正多角形の作図（2021年度・修士論文）
• 正絡み目のHOMFLY多項式について（2021年度・修士論文）
• 幅が5以下の結び目のJones多項式（2020年度・修士論文）
• 3つの不変量と2橋結び目の族（2020年度・修士論文）
• θ-曲線と山田多項式（2019年度・修士論文）
• 自明な0番ホムフリー係数多項式を持つ結び目の族（2018年度・修士論文）
• ブレイド指数４の４成分絡み目のホムフリー多項式について（2017年度・修士論文）

教員情報

E-mail：　miyazawa@（@以下はyamaguchi-u.ac.jp）