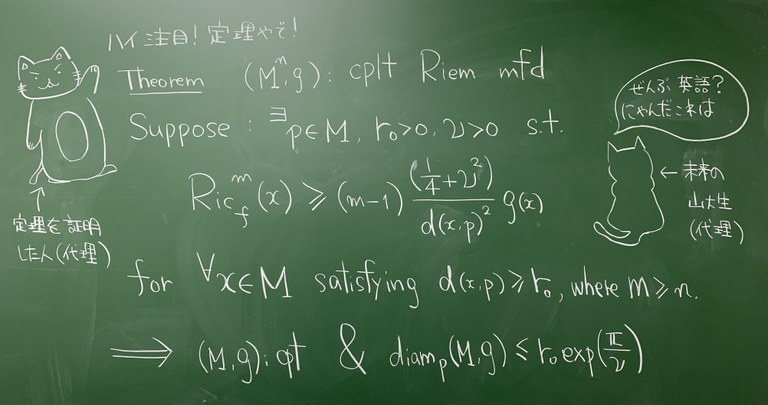
研究テーマ

リーマン多様体上の幾何解析学

研究内容

私は幾何学の中でも微分幾何学と呼ばれる分野を研究しています。大雑把に言うと、微分幾何学とは我々の宇宙空間がどういった形をしているかという問いに深い繋がりがある学問で、「多様体」と呼ばれる空間を微分積分学や線形代数学を駆使して調べる学問のことです。ここで「多様体」とは曲線や曲面を高次元の概念に一般化したものです。曲線は1次元の多様体で、曲面は2次元の多様体になります。特に私は「多様体」の中でも「リーマン多様体」と呼ばれる対象を研究しています。リーマン多様体とは空間の2点間の長さを測る物差しのようなものが備わった多様体のことで、ユークリッド空間や球面はリーマン多様体の具体例になっています。私は「リーマン多様体」の中でもアインシュタインの相対性理論と縁が深いアインシュタイン多様体に興味を持ち、アインシュタイン多様体や Ricci ソリトンと呼ばれるアインシュタイン多様体の一般化に対して、それらの直径や体積がどのような振る舞いをするかなどを調べています。

海外研究滞在中に撮った動物たちで、それぞれ台北の猫（台湾）、ジブラルタルの猿（イギリス）、ブリスベンのコアラ（オーストラリア）、カイロのラクダ（エジプト）、ムンバイの犬（インド）、台北のパンダ（台湾）です。みんなかわいいですね。

指導学生の修士論文・卒業論文題目

• 多様体論（2021年度・卒業論文）

教員情報