研究テーマ

3次元トポロジーにおけるトーション不変量の研究

研究内容

私の研究分野は位相幾何学で、主な研究対象は3次元多様体です。例えば、私たちは自分の周りの空間を3次元（ユークリッド）空間と捉えていますが、宇宙全体がどのような形をしているかは局所的な情報のみからは決定できず、様々な全体像が考えられます。このように局所的には3次元空間と見做せるような空間のことを3次元多様体といいます。3次元多様体に関しては、その基本群の性質と幾何構造との間に深い関係があることが知られています。ここで基本群とは、多様体内の閉曲線の集合で、「連続的に変形」して移り合うものは同じとみなし、さらに、閉曲線同士を「つなぎあわせる」操作を演算として導入した群のことです。基本群と多様体構造の研究方法は多くありますが、私は基本群から定義される、ライデマイスタートーションと呼ばれる位相不変量を研究しています。ライデマイスタートーションは3次元幾何構造との関連性において興味深い性質がいくつか予見されおり、それらに着目して研究を行っています。 

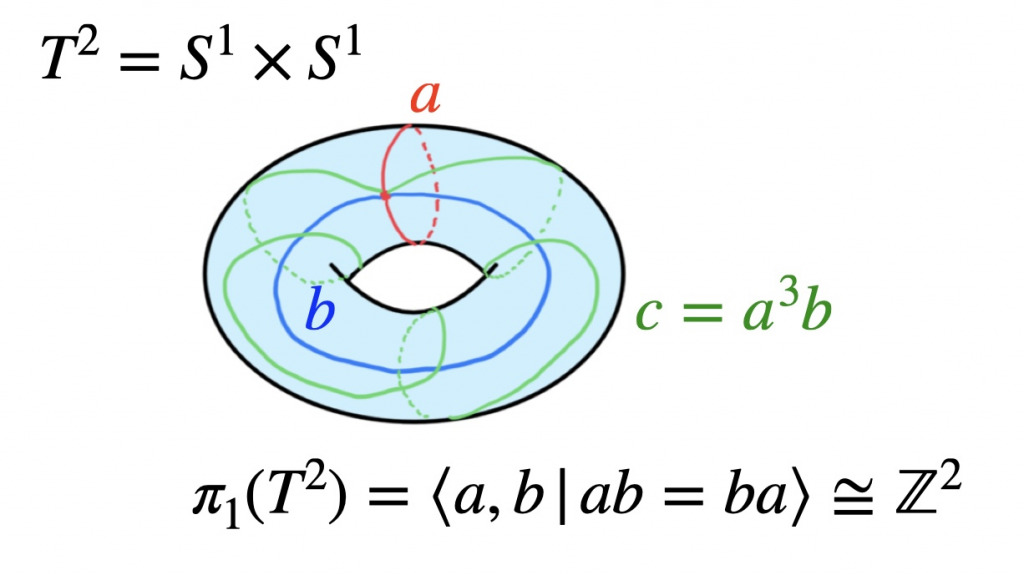「ドーナツの表面」の基本群

教員情報

E-mail：　wakijo@（@以下はyamaguchi-u.ac.jp）